强化学习 - 马尔可夫决策过程与强化学习

Created in July 15, 2025

2025   ·   RL   math   ·   reinforcement-learning

什么是强化学习？

强化学习是机器学习的一个领域，其灵感来自行为主义心理学，研究智能体如何从与环境的互动中学习。
—Sutton & Barto (1998), Phil, 维基百科

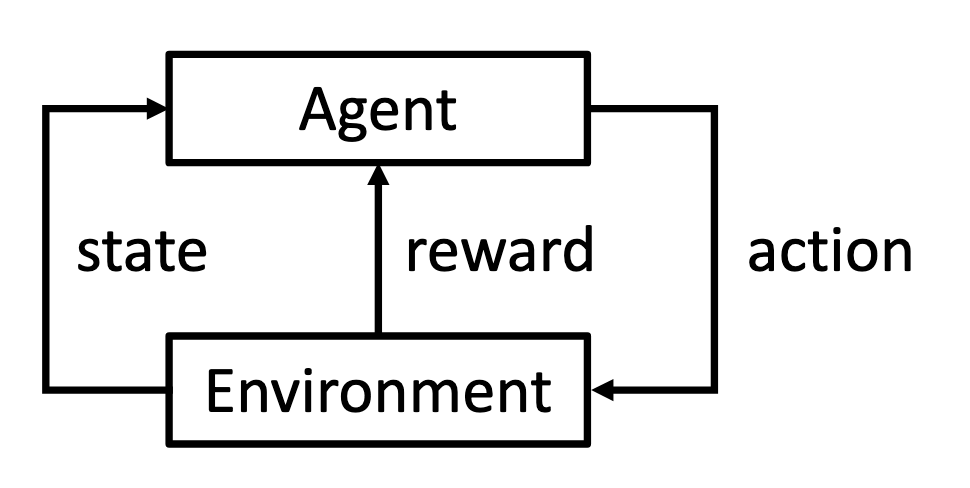
一个典型的强化学习系统由5个部分组成：智能体（agent）在环境（environment）中的每个状态（state）下执行一个动作（action），并在满足某些标准时获得奖励（reward）。

监督学习问题可以转化为强化学习问题吗？ 可以。我们可以将一个监督学习问题转化为一个强化学习问题（状态作为分类器的输入；动作作为标签；如果标签正确，奖励为1，否则为-1）。
强化学习是监督学习的替代品吗？

不是。监督学习使用指导性反馈（智能体应该采取什么行动）。任何偏离所提供反馈的行为都会受到惩罚。

另一方面，强化学习问题不是以固定的数据集形式提供的，而是以代码或整个环境的描述形式提供的。强化学习中的奖励应该传达智能体的行为有多“好”，而不是最好的行为应该是什么。智能体的目标是最大化总奖励，这可能需要智能体放弃眼前的奖励以获得以后更大的奖励。

如果你有一个序列问题或一个只有评估性反馈可用的问题（或两者兼有！），那么你应该考虑使用强化学习。

示例：网格世界

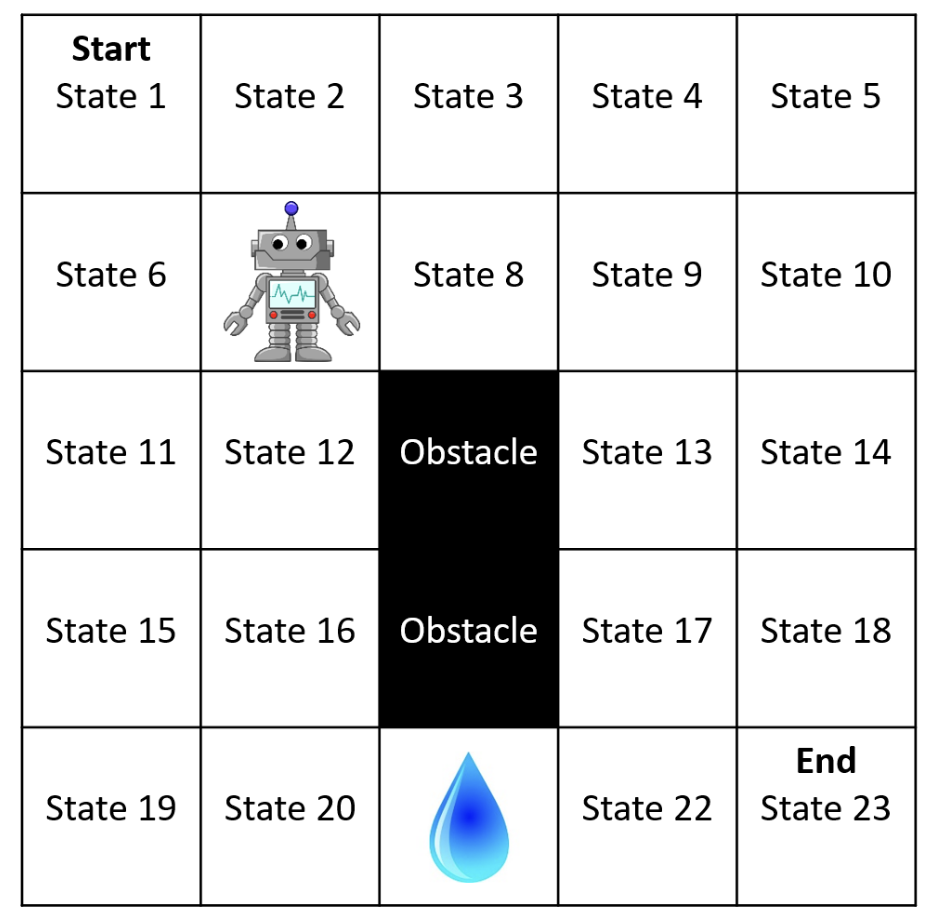
状态: 机器人的位置。机器人没有朝向。

动作: 尝试向上 (AU), 尝试向下 (AD), 尝试向左 (AL), 尝试向右 (AR)

环境动态:

奖励:

  • 智能体进入有水的状态会得到-10的奖励，进入目标状态会得到+10的奖励。
  • 进入任何其他状态的奖励为零。
  • 任何导致智能体停留在状态21的动作都将被视为再次进入水域状态，并导致额外的-10奖励。
  • 奖励折扣参数 \(\gamma = 0.9\)。

状态数量: 24

  • 23个正常状态 + 1个终止吸收状态 (\(s_\infty\))
    • 一旦进入\(s_\infty\)，智能体就永远无法离开（回合结束）。
    • \(s_\infty\) 不应被认为是“目标”状态。

用数学方式描述智能体和环境

环境的数学定义

我们可以使用马尔可夫决策过程（MDPs）来形式化强化学习问题的环境。其中的独特术语是\(\mathcal{S}\)（所有可能状态的集合），\(\mathcal{A}\)（所有可能动作的集合），\(p\)（转移函数），\(d_R\)（奖励分布），\(R\)（奖励函数），\(d_0\)（初始状态分布）和\(\gamma\)（奖励折扣参数）。环境的通用定义是

\[(\mathcal{S}, \mathcal{A}, p, R, \gamma)\]

智能体的数学定义

我们将智能体选择动作的决策规则定义为策略。形式上，策略\(\pi\)是一个函数

\[\begin{aligned} &\pi : \mathcal{S} \times \mathcal{A} \rightarrow [0,1] \\ &\pi(s,a) := \text{Pr}(A_t=a | S_t=s) \end{aligned}\]

智能体的目标

智能体的目标是找到一个最优策略\(\pi^*\)，以最大化智能体将获得的总奖励的期望值。

示例：山地车

山地车环境
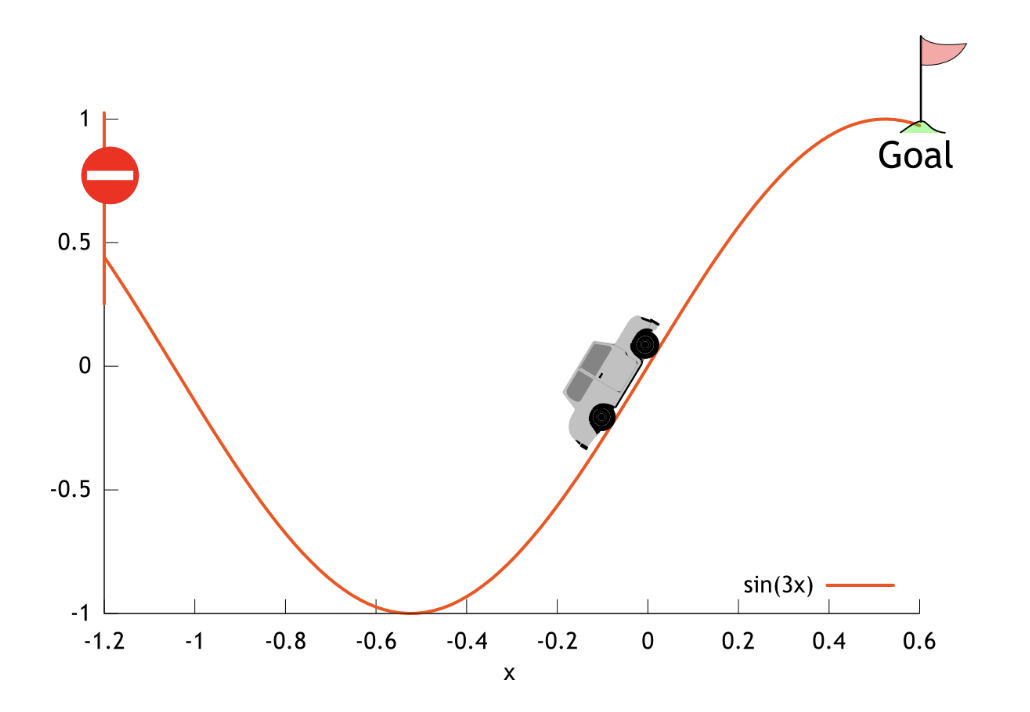
  • 状态: \(s=(x,v)\), 其中 \(x \in \mathbb{R}\) 是小车的位置，\(v \in \mathbb{R}\) 是速度。
  • 动作: \(a \in \{\texttt{倒车}, \texttt{空挡}, \texttt{前进}\}\). 这些动作被映射为数值 \(a \in \{-1, 0 ,1\}\)。

  • 动态: 动态是确定性的——在状态\(s\)下采取动作\(a\)总是产生相同的状态\(s^\prime\)。因此，\(p(s,a,s^\prime) \in \{0, 1\}\)。动态特性如下：

    \[\begin{aligned} v_{t+1} &= v_t + 0.001 a_t - 0.0025 \cos(3x_t) \\ x_{t+1} &= x_t + v_{t+1} \end{aligned}\]

    在计算出下一个状态 \(s^\prime = [x_{t+1}, v_{t+1}]\) 后，

    • \(x_{t+1}\) 的值被限制在闭区间 \([-1.2, 0.5]\) 内。
    • \(v_{t+1}\) 的值被限制在闭区间 \([-0.7, 0.7]\) 内。
    • 如果 \(x_{t+1}\) 到达左边界或右边界（\(x_{t+1} = -1.2\) 或 \(x_{t+1} = 0.5\)），那么小车的速度将重置为零（\(v_{t+1} = 0\)）。
  • 初始状态: \(S_0 = (X_0, 0)\), 其中 \(X_0\) 是从区间 \([-0.6, -0.4]\) 中均匀随机抽取的初始位置。
  • 终止状态: 如果 \(x_t = 0.5\)，则该状态为终止状态（它总是转移到 \(s_\infty\)）。
  • 奖励: \(R_t\) 总是为 -1，除非转移到 \(s_\infty\)（从 \(s_\infty\) 或从终止状态），此时 \(R_t = 0\)。
  • 折扣: \(\gamma = 1.0\)。

附加术语、符号和假设

  • 历史（history），\(H_t\)，是回合中直到时间\(t\)所发生事件的记录：

    \[H_t := (S_0, A_0, R_0, S_1, A_1, R_1, \ldots, S_t, A_t, R_t)\]
  • 轨迹（trajectory）是整个回合的历史：\(H_\infty\)
  • 轨迹的回报（return）或折扣回报（discounted return）是奖励的折扣总和 \(G := \sum_{t = 0}^{\infty} \gamma^t R_t\)
  • 期望回报（expected return）或期望折扣回报（expected discounted return）可以写成 \(J(\pi) := \mathbf{E}[G\vert\pi]\)
  • 从时间\(t\)开始的回报或从时间\(t\)开始的折扣回报，\(G_t\)，是从时间\(t\)开始的奖励的折扣总和
\[G_t := \sum_{k=1}^{\infty} \gamma^k R_{t+k}\]

  • MDP的范围（horizon），\(L\)，是满足以下条件的最小整数

    \[\forall t \geq L, \text{Pr}(S_t = s_\infty) = 1\]
    • 如果对于所有策略 \(L < \infty\)，我们称该MDP为有限范围（finite horizon）
    • 如果 \(L = \infty\)，则该领域可能是不确定范围（indefinite horizon）（智能体总是会进入\(s_\infty\)）或无限范围（infinite horizon）（智能体可能永远不会进入\(s_\infty\)）

马尔可夫性质

马尔可夫性质 (马尔可夫假设)

简而言之：给定现在，未来与过去无关。

形式上，给定\(S_t\)，\(S_{t+1}\) 条件独立于 \(H_{t-1}\)。也就是说，对于所有的 \(h, s, a, s^\prime, t\)：

\(\text{Pr}(S_{t+1} = s^\prime | H_{t-1} = h, S_{t}=s, A_{t}=a) = \text{Pr}(S_{t+1}=s^\prime | S_{t}=s, A_{t}=a)\)

如果一个模型（环境、奖励…）满足马尔可夫假设，我们就说它具有马尔可夫性质，或者说这个模型是 Markovian的。

为什么在强化学习中使用MDP？

MDP不仅功能强大，足以模拟学习智能体与其环境之间的交互，它还带来了一些关键的保证，使我们的“强化学习”能够真正起作用。

现在，让我们跳过推导，直接看结论。

最优策略的存在性

对于所有满足 \(|\mathcal{S}| < \infty\), \(|\mathcal{A}| < \infty\), \(R_\text{max} < \infty\) 和 \(\gamma < 1\) 的MDP，至少存在一个最优策略 \(\pi^*\)。

稍后当我们介绍贝尔曼方程和贝尔曼最优方程时，我们将进一步确定：

  1. 如果一个策略\(\pi\)在每个步骤中都达到了一个状态，其期望的未来奖励无法通过任何其他行动或决策进一步提高（贝尔曼最优方程），那么它就是一个最优策略。
  2. 如果只有有限数量的可能状态和动作，奖励有界，并且未来奖励被折扣（折扣因子\(\gamma < 1\)），那么存在一个满足贝尔曼最优方程的策略\(\pi\)。

此外，我们可以使用贝尔曼方程和贝尔曼最优方程执行策略/价值迭代（稍后将介绍）。因此，我们不仅可以一次又一次地迭代得到更好的策略，而且在某些约束下，还可以证明最终策略将收敛到最优策略。