强化学习 — 价值函数
在上一节中,我们介绍了马尔可夫决策过程(MDP)如何融入强化学习。本章将基于 MDP 的定义,展示如何从数学角度评估 RL 智能体。
状态价值函数
状态价值函数 \(v^\pi(s)\) 表示当智能体从状态 \(s\) 出发并按照策略 \(\pi\) 行动时,其期望折扣回报。通俗地说,它衡量在采用策略 \(\pi\) 时身处状态 \(s\) “有多好”。我们称 \(v^\pi(s)\) 为状态 \(s\) 的价值。
\[\begin{aligned} v^\pi(s) &:= \mathbf{E}\ \Bigg[\underbrace{\sum_{k=0}^{\infty}\gamma^k R_{t+k}}_{G_t} \bigg| S_t=s, \pi\ \Bigg] \\ &:= \mathbf{E}[G_t|S_t=s, \pi] \\ &:= \mathbf{E}\ \Bigg[\sum_{t=0}^{\infty}\gamma^k R_{t} \bigg| S_0=s, \pi\ \Bigg] \end{aligned}\]回顾我们在上一节中使用的 \(G_t\)(从时间步 \(t\) 开始的折扣回报)记号,可以发现这正是其等价形式。
一个简单的 MDP 示例
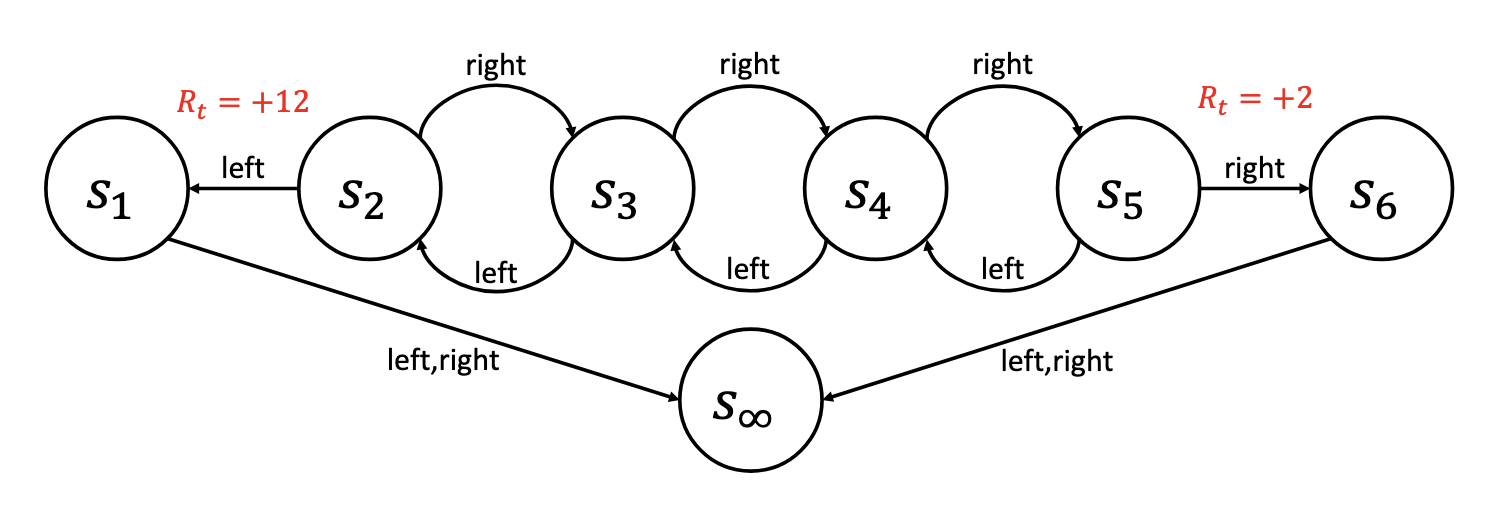
在上图所示的 MDP 中,智能体每次可选择两个动作中的一个:Left 或 Right。在状态 \(s_1\) 与 \(s_6\) 中,无论采取何种动作都会直接转移至终止状态 \(s_\infty\)。只有在发生 \(s_2 \to s_1\) 或 \(s_5 \to s_6\) 的转移时,智能体才能获得奖励。为简化计算,设折扣因子 \(\gamma = 0.5\)。
我们为该 MDP 尝试两种策略:策略 \(\pi_1\) 始终选择 Left;策略 \(\pi_2\) 始终选择 Right。
策略 1(\(\pi_1\)):始终选择 Left
- \(v^{\pi_1}(s_1) = 0\) (始终直接进入终止状态)
- \(v^{\pi_1}(s_2) = 12\gamma^0 = 12\).
- \(v^{\pi_1}(s_3) = 0\gamma^0 + 12\gamma^1 = 6\).
- \(v^{\pi_1}(s_4) = 0\gamma^0 + 0\gamma^1 + 12\gamma^2 = 3\).
- \(v^{\pi_1}(s_5) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 12\gamma^3 = 1.5\).
- \(v^{\pi_1}(s_6) = 0\).
策略 2(\(\pi_2\)):始终选择 Right
- \(v^{\pi_2}(s_1) = 0\).
- \(v^{\pi_2}(s_2) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 2\gamma^3 = 0.25\).
- \(v^{\pi_2}(s_3) = 0\gamma^0 + 0\gamma^1 + 2\gamma^2 = 0.5\).
- \(v^{\pi_2}(s_4) = 0\gamma^0 + 2\gamma^1 = 1\).
- \(v^{\pi_2}(s_5) = 2\gamma^0 = 2\).
- \(v^{\pi_2}(s_6) = 0\).
行动价值函数
行动价值函数 \(q^\pi(s,a)\)(亦称 Q‑函数)表示当智能体在状态 \(s\) 采取动作 \(a\) 并随后按照策略 \(\pi\) 行动时,其期望折扣回报。
\[\begin{aligned} q^\pi(s,a) &:= \mathbf{E}\ \Bigg[\sum_{k=0}^{\infty}\gamma^k R_{t+k} \bigg| S_t=s, A_t = a, \pi\ \Bigg] \\ &:= \mathbf{E}[G_t|S_t=s, A_t=a, \pi] \\ &:= \mathbf{E}\ \Bigg[\sum_{t=0}^{\infty}\gamma^k R_{t} \bigg| S_0=s, A_0=a, \pi\ \Bigg] \end{aligned}\]👀再看MDP

策略 1(\(\pi_1\)):始终选择 Left
- \(q^{\pi_1}(s_1, L) = 0\).
- \(q^{\pi_1}(s_1, R) = 0\).
- \(q^{\pi_1}(s_2, L) = 12\gamma^0 =12\).
- \(q^{\pi_1}(s_2, R) = 0\gamma^0 + 0\gamma^1 + 12\gamma^2 = 3\).
- \(q^{\pi_1}(s_3, L) = 0\gamma^0 + 12\gamma^1 = 6\).
- \(q^{\pi_1}(s_3, R) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 12\gamma^3 = 1.5\).
- \(q^{\pi_1}(s_4, L) = 0\gamma^0 + 0\gamma^1 + 12\gamma^2 = 3\).
- \(q^{\pi_1}(s_4, R) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 0\gamma^3 + 12\gamma^4 = 0.75\).
- \(q^{\pi_1}(s_5, L) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 12\gamma^3 = 1.5\).
- \(q^{\pi_1}(s_5, R) = 2\gamma^0 = 2\).
- \(q^{\pi_1}(s_6, L) = 0\).
- \(q^{\pi_1}(s_6, R) = 0\).
策略 2(\(\pi_2\)):始终选择 Right
- \(q^{\pi_2}(s_1, L) = 0\).
- \(q^{\pi_2}(s_1, R) = 0\).
- \(q^{\pi_2}(s_2, L) = 12\gamma^0 =12\).
- \(q^{\pi_2}(s_2, R) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 2\gamma^3 = 0.25\).
- \(q^{\pi_2}(s_3, L) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 0\gamma^3 + 2\gamma^4 = 0.125\).
- \(q^{\pi_2}(s_3, R) = 0\gamma^0 + 0\gamma^1 + 2\gamma^2 = 0.5\).
- \(q^{\pi_2}(s_4, L) = 0\gamma^0 + 0\gamma^1 + 0\gamma^2 + 2\gamma^3 = 0.25\).
- \(q^{\pi_2}(s_4, R) = 0\gamma^0 + 2\gamma^1 = 1\).
- \(q^{\pi_2}(s_5, L) = 0\gamma^0 + 0\gamma^1 + 2\gamma^2 = 0.5\).
- \(q^{\pi_2}(s_5, R) = 2\gamma^0 = 2\).
- \(q^{\pi_2}(s_6, L) = 0\).
- \(q^{\pi_2}(s_6, R) = 0\).
\(v^\pi\) 的贝尔曼方程
状态价值函数的贝尔曼方程是 \(v^\pi\) 的递归表达式。为推导该方程,我们首先将即时奖励从价值函数中分离出来:
\[\begin{aligned} v^\pi(s) &:= \textbf{E}\left[\sum_{k=0}^{\infty}\gamma^k R_{t+k} \bigg\vert S_t=s, \pi\right] \\ &= \textbf{E}\left[R_t + \sum_{k=1}^{\infty}\gamma^k R_{t+k} \bigg\vert S_t=s, \pi\right] \\ &= R_t + \textbf{E}\left[\gamma\sum_{k=1}^{\infty}\gamma^{k-1} R_{t+k} \bigg\vert S_t=s, \pi\right] \end{aligned}\]通过将求和索引调整为从 0 开始(即将所有 \(k\) 替换为 \(k+1\)),可得到
\[\begin{aligned} \textbf{E}\left[\gamma\sum_{k=1}^{\infty}\gamma^{k-1} R_{t+k} \bigg\vert S_t=s, \pi\right] = \textbf{E}\left[\gamma\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg\vert S_t=s, \pi\right] \end{aligned}\]根据全概率公式 \(\textbf{E}[X] = \textbf{E}[\textbf{E}[X \vert Y]]\),令首次动作 \(A_t=a\) 及下一状态 \(S_{t+1}=s'\) 作为条件变量,可得
\[\begin{aligned} &\textbf{E}\left[\gamma\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg\vert S_t=s, \pi\right] \\ = &\sum_{a\in\mathcal{A}}\pi(s,a)\sum_{s' \in \mathcal{S}}p(s,a,s') \, \textbf{E}\left[\gamma\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg\vert S_t=s, A_t=a, S_{t+1}=s', \pi\right] \end{aligned}\]利用马尔可夫性质,可将条件中的 \(S_t\) 和 \(A_t\) 去掉:
\[\begin{aligned} &\textbf{E}\left[\gamma\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg\vert S_{t+1}=s^\prime, \pi\right] \\ = &\sum_{a\in\mathcal{A}}\pi(s,a)\sum_{s' \in \mathcal{S}}p(s,a,s') \, \gamma\textbf{E}\left[\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg\vert S_{t+1}=s', \pi\right] \end{aligned}\]根据状态价值函数定义,最后一项正是 \(v^\pi(s')\):
\[\begin{aligned} &\textbf{E}\left[\gamma\sum_{k=0}^\infty \gamma^k R_{t+k+1} \bigg\vert S_t=s, \pi\right] \\ = & \gamma\sum_{a\in\mathcal{A}}\pi(s,a)\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime) v^\pi(s^\prime) \end{aligned}\]由于对任意给定 \(s\)、\(a\),转移到下一状态 \(s'\) 的概率之和为 1,可将即时奖励写成
\[\begin{aligned} R_t = \sum_{a\in\mathcal{A}}\pi(s,a)R(s,a) = \sum_{a\in\mathcal{A}}\pi(s,a)\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)R(s,a) \end{aligned}\]综合可得
\[\begin{aligned} v^\pi(s) &= R_t + \textbf{E}\left[\gamma\sum_{k=0}^\infty \gamma^k R_{t+k+1} \bigg\vert S_t=s, \pi\right] \\ &= \sum_{a\in\mathcal{A}}\pi(s,a)\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)R(s,a) + \sum_{a\in\mathcal{A}}\pi(s,a)\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime) \gamma v^\pi(s^\prime) \end{aligned}\]最终,可得到简洁形式
\[v^\pi(s) = \boxed{\sum_{a\in\mathcal{A}}\pi(s,a)\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\big(R(s,a) +\gamma v^\pi(s^\prime)\big)}\]关于贝尔曼方程的优点
我们可以将贝尔曼方程视为把期望回报拆分为两部分:
- 下一时间步获得的奖励(即时奖励)
- 下一状态的价值
原始定义需要考虑整条状态序列,而贝尔曼方程只需向前看一步。
- 贝尔曼方程的递归性质使其在计算上更有帮助
\(q^\pi\) 的贝尔曼方程
就如 \(v^\pi\) 的贝尔曼方程给出了 \(v^\pi\) 的递归关系一样,\(q^\pi\) 的贝尔曼方程则给出了行动价值函数 \(q^\pi\) 的递归关系:
\[\begin{aligned} q^\pi(s,a) &:= \mathbf{E}\Bigg[\sum_{k=0}^{\infty}\gamma^k R_{t+k} \bigg| S_t=s, A_t = a, \pi\Bigg] \\ &= R_t + \textbf{E}\left[\gamma\sum_{k=0}^\infty \gamma^k R_{t+k+1} \bigg\vert S_t=s, A_t = a, \pi\right] \\ &= R_t + \sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\sum_{a^\prime \in \mathcal{A}} \pi(s^\prime,a^\prime)\times\textbf{E}\left[\gamma\sum_{k=0}^\infty \gamma^k R_{t+k+1} \bigg\vert S_t=s, A_t = a, S_{t+1}=s^\prime, A_{t+1}=a^\prime, \pi\right] \\ &= R_t + \sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\sum_{a^\prime \in \mathcal{A}}\pi(s^\prime,a^\prime) \times\textbf{E}\left[\gamma\sum_{k=0}^\infty \gamma^k R_{t+k+1} \bigg\vert S_{t+1}=s^\prime, A_{t+1}=a^\prime, \pi\right] \\ &= R_t + \sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\sum_{a^\prime \in \mathcal{A}}\pi(s^\prime,a^\prime)\gamma q^\pi(s^\prime, s^\prime) \\ &= \boxed{R(s,a) + \gamma\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\sum_{a^\prime \in \mathcal{A}}\pi(s^\prime,a^\prime)q^\pi(s^\prime, a^\prime)} \end{aligned}\]或简写为
\[q^\pi(s,a) = \boxed{R(s,a) + \gamma\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\sum_{a^\prime \in \mathcal{A}}\pi(s^\prime,a^\prime)q^\pi(s^\prime, a^\prime)}\]最优价值函数
最优策略 \(\pi^*\)
若某策略 \(\pi^*\) 至少与所有其他策略一样好,则称其为最优策略。即
即便最优策略可能不唯一,最优价值函数 \(v^*\) 与 \(q^*\) 却是唯一的——所有最优策略共享同一状态价值函数与行动价值函数。
已知最优状态价值函数,若未知转移概率及奖励函数,能否求得最优策略?
不能。 $$ \arg\max_{a\in\mathcal{A}}\sum_{s'}p(s,a,s')\big[R(s,a) + \gamma v^\pi(s')\big] $$ 的计算仍依赖于 p 和 R。
已知最优行动价值函数,若未知转移概率及奖励函数,能否求得最优策略?
可以。 $$ \arg\max_{a\in\mathcal{A}}q^*(s,a) $$ 即为状态 s 下的最优动作。
\(v^*\) 的贝尔曼最优方程
从贝尔曼方程出发,
\[v^*(s) = \sum_{a\in\mathcal{A}}\pi^*(s,a)\sum_{s' \in \mathcal{S}}p(s,a,s')\big[R(s,a) + \gamma v^*(s')\big]\]由于最优策略 \(\pi^*\) 仅选择能最大化 \(q^*(s,a)\) 的动作,可写为
\[v^*(s) = \max_{a\in\mathcal{A}}\sum_{s' \in \mathcal{S}}p(s,a,s')\big[R(s,a) + \gamma v^*(s')\big]\]这就是 \(v^*\) 的贝尔曼最优方程。
若一个策略 \(\pi\) 满足贝尔曼最优方程,则对所有状态 \(s \in \mathcal{S}\) 有
\[v^*(s) = \max_{a\in\mathcal{A}}\sum_{s' \in \mathcal{S}}p(s,a,s')\big[R(s,a) + \gamma v^*(s')\big]\]\(q^*\) 的贝尔曼最优方程
若一个策略 \(\pi\) 满足贝尔曼最优方程,则对所有动作 \(a \in \mathcal{A}\) 有
\[q^*(s,a) = \sum_{s' \in \mathcal{S}} p(s,a,s')\left[ R(s,a) + \gamma \max_{a'\in\mathcal{A}}q^*(s', a')\right]\]贝尔曼最优方程与最优策略
若策略 \(\pi\) 满足贝尔曼最优方程,则 \(\pi\) 为最优策略。
证明:
假设一个策略 \(\pi\) 满足贝尔曼最优方程,那么对于所有状态 \(s\):
\[v^\pi(s) = \max_{a \in \mathcal{A}}\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)[R(s,a) + \gamma v^\pi(s^\prime)]\]我们可以将贝尔曼最优方程递归地代入表达式中,并替换 \(v^\pi(s^\prime)\):
\[v^\pi(s) = \max_{a \in \mathcal{A}}\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\left[R(s,a) + \gamma \left(\max_{a^\prime \in \mathcal{A}}\sum_{s^{\prime\prime}}p(s^\prime, a^\prime, s^{\prime\prime})(R(s^\prime, a^\prime) + \gamma v^\pi(s^{\prime\prime})\right)\right]\]我们可以无限地继续这个过程,直到 \(\pi\) 从表达式中完全消失:
\[v^\pi(s) = \max_{a \in \mathcal{A}}\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\left[R(s,a) + \gamma \left(\max_{a^\prime \in \mathcal{A}}\sum_{s^{\prime\prime}}p(s^\prime, a^\prime, s^{\prime\prime})(R(s^\prime, a^\prime) + \gamma \ldots\right)\right]\]在每个时间步 \(t\),选择的动作都是最大化未来期望折扣回报的动作,前提是未来的动作也是为了最大化未来折扣回报。
现在,让我们考虑任何一个新的策略 \(\pi^\prime\)。如果我们将 \(\max_{a \in \mathcal{A}}\) 替换为 \(\sum_{a \in \mathcal{A}}\pi^\prime(s,a)\),关系会怎样?我们认为表达式的值不会变得比之前更大。也就是说,对于任何策略 \(\pi^\prime\):
\[\begin{aligned} v^\pi(s) &= \max_{a \in \mathcal{A}}\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\left[R(s,a) + \gamma \left(\max_{a^\prime \in \mathcal{A}}\sum_{s^{\prime\prime}}p(s^\prime, a^\prime, s^{\prime\prime})(R(s^\prime, a^\prime) + \gamma \ldots\right)\right] \\ &\geq \sum_{a \in \mathcal{A}}\pi^\prime(s,a)\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\left[R(s,a) + \gamma \left(\sum_{a^\prime \in \mathcal{A}}\pi^\prime(s^\prime,a^\prime)\sum_{s^{\prime\prime}}p(s^\prime, a^\prime, s^{\prime\prime})(R(s^\prime, a^\prime) + \gamma \ldots\right)\right] \end{aligned}\]鉴于上述不等式对所有策略 \(\pi^\prime\) 都成立,我们得出对于所有状态 \(s \in \mathcal{S}\) 和所有策略 \(\pi^\prime \in \Pi\):
\[\begin{aligned} v^\pi(s) &= \max_{a \in \mathcal{A}}\sum_{s^\prime \in \mathcal{S}}p(s,a,s^\prime)\left[R(s,a) + \gamma \left(\max_{a^\prime \in \mathcal{A}}\sum_{s^{\prime\prime}}p(s^\prime, a^\prime, s^{\prime\prime})(R(s^\prime, a^\prime) + \gamma \ldots\right)\right] \\ &\geq \mathbf{E}[G_t | S_t = s, \pi^\prime] \\ &= v^{\pi^\prime}(s) \end{aligned}\]因此,对于所有状态 \(s \in \mathcal{S}\) 和所有策略 \(\pi^\prime \in \Pi\),\(v^\pi(s) \geq v^{\pi^\prime}(s)\)。换句话说,对于所有策略 \(\pi^\prime \in \Pi\),我们有 \(\pi \geq \pi^\prime\),因此 \(\pi\) 是一个最优策略。